Our research focuses in the low-dimensional electronic nanostructures, more precisely in the so-called designer atoms or quantum dots (QDs). Modern techniques in constructing ultrasmall semiconductor devices have made it possible to confine electrons in the three dimensions, so that the quantization of its energy and charge is easily observable. The fabrication of these devices can be performed, for example, by combining pure and doped semiconductor thin layers. In normal semiconductors, such as GaAs or AlGaAs, the electrons move freely in all dimensions, and there is no quantization of the energy levels. In the QDs, electrons are usually trapped into a two dimensional (2D) gas in the interface between two differently doped materials. Additionally to the 2D gas there might appear a effective confinement wich will make the electrons behave like if they were in an artificial atom.
In order to solve the nonrelativistic Schrödinger equation that describes or quantum system, we make use of the mathematical model named configuration interaction (CI) also known as exact diagonalization method. This method is limited by the number of particles present in the system. Actually we are not applying it to systems bigger than four electrons with the resulting (sparse) hamiltonian matrix being of the order of 105.

The first step is to write the many-body Hamiltonian taking into account the interparticle interactions (electrostatic potential), the external fields (magnetic field is present), Rashba coupling and
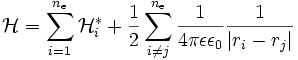
where ℋ* is the single-particle Hamiltonian operator explicitly written as:
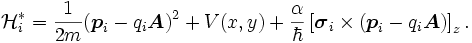
The confinement potential is modeled by a group of Gaussians[1]
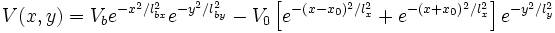
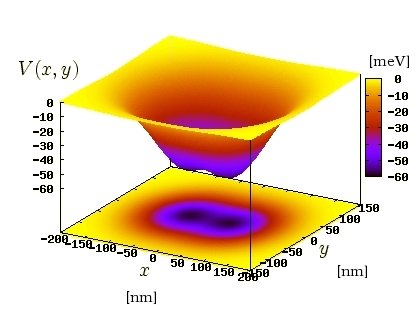
with all the unkown parameters being positive. It should be appreciated the broken symmetry between x and y axes, so we are working with elliptically shaped QDs. In the contiguous figure, we have plotted our actually studied system. It has an interdot barrier of 3 meV and a separation of 80 nm between dots and spread of the same magnitude for each of the single dot. The part in the Hamiltonian wich takes into account the interaction (Coulomb interaction) is, computationally, the toughest bottleneck[2], as it includes the evaluation of fourfold summations with up to thousands of elements.
Back to theory page
![]()