We study quasiparticle dynamics in 3He-4He mixtures at low temperatures. In dilute mixtures the 3He part of the mixture behaves as a degenerate Fermi liquid, and can be described by Landau's Fermi liquid theory, treating collective exitation modes of 3He system as quasiparticles, which have definite energy and momentum. The superfluid 4He part acts as a background, and its velocity affects quasiparticle energy [1].
The properties of helium mixtures can be studied experimentally using vibrating wire resonators immersed in the liquid. The liquid damps the vibration of the wire, causing dissipation and a change to the effective inertia of the wire, which can be measured at different temperatures. As temperature is reduced, the viscocity of 3He increases, thus increasing the inertia of the wire, as more fluid moves along with it. The increased inertia is observed as decrease in the resonant frequency of the wire. When temperature is further reduced, the mean free path of quasiparticles exceeds the size of the experimental setup, and the resonant frequency of the wire begins to increase. Close to the zero temperature the mean free path becomes infinite, and the fluid can be described as a gas of ballistic quasiparticles. In recent experiments the resonant frequency, in the ballistic limit, surprisingly becomes less than that caused by the superfluid 4He alone [2]. This is one motive for our theoretical research of the subject.

We solve numerically the Landau-Boltzmann equation for 3He quasiparticles in a discrete grid near the wire for different values of the mean free path. The effect of the wire is taken into account by using boundary condition for quasiparticle scattering from the surface of the wire. Both specular and diffusive scattering, or their combination, can be used. We have included the effect of Fermi liquid interactions, and the superfluid motion of 4He in the calculations. The confinement of the fluid is taken into account by assuming either diffusive or absorbing walls of the helium container. To mimic the geometry of the experiments we use a slab geometry, where the wire oscillates between two plane walls. For comparison, we use a cylindrical container (of radius b), concentric with the wire (radius a).
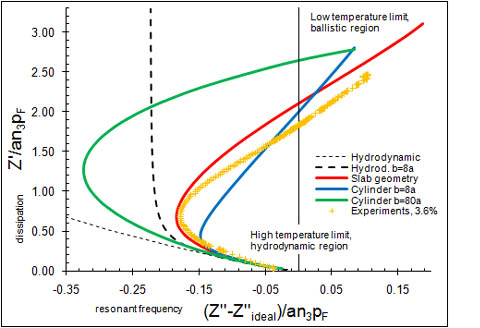
Once the quasiparticle distribution is solved, the force on the wire can be readily calculated. The results can be conveniently presented in terms of the mechanical impedance Z, using F=Zu, where u is the velocity of the wire. The results are shown in the figure on the left. The red line shows the main results in the slab geometry for diffuse wire and walls, the blue line shows results for a cylindrical container of radius b=8a with absorbing walls, and the green line is the same with radius b=80a. These are compared with the experimental results of Martikainen et al.[2] (yellow crosses), and with hydrodynamic theory (thin dashed line for unlimited fluid and thick dashed line for a cylindrical container of radius b=8a). The parameters for all calculations in the figure correspond to a 3.6% helium mixture, and are obtained from independent measurements.
Our results show rather satisfactory agreement with experiments, taking
into account that no fitting parameters have been used. Especially, they
confirm that in the ballistic limit, the resonant frequency of the wire
becomes larger than at the high temperature end. Part of this overshoot
can be explained by noting that the normal component of the fluid (the 3He part plus some of the 4He)
decouples from the wire. The rest is explained by the Fermi liquid
interactions and the confiment. The fermi liquid acts like an elastic
medium, leading to increase of the oscillation frequency of the wire.
Back to theory page
09.06.2011, Timo Virtanen