3_ratkaisu.html

Valmiit funktiot

Kokeile mitä antaa

In[1]:=

Out[1]=

In[2]:=

Out[2]=

In[3]:=

Out[3]=

In[4]:=

Out[4]=

In[5]:=

Out[5]=

In[6]:=

Out[6]=

In[7]:=

Out[7]=

In[8]:=

Out[8]=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=

In[12]:=

Out[12]=

In[13]:=

Out[13]=

In[14]:=

Out[14]=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

In[17]:=

Out[17]=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

In[20]:=

In[21]:=

Out[21]=

Out[22]=

Out[23]=

In[24]:=

[Graphics:HTMLFiles/3_ratkaisu_55.gif]

Out[24]=

[Graphics:HTMLFiles/3_ratkaisu_57.gif]

Out[25]=

[Graphics:HTMLFiles/3_ratkaisu_59.gif]

Out[26]=

[Graphics:HTMLFiles/3_ratkaisu_61.gif]

Out[27]=

Omat funktiot

Määrittele funktio f(x)=x^2+2x. Laske funktion arvo kun x=3.

In[28]:=

Out[29]=

Etsi edellä määritellyn funktion nollakohdat.

In[30]:=

Out[30]=

Määrittele f(x)=-3x+ Mathematica'ssa ja piirrä sen kuvaaja välillä [-3,3].

In[33]:=

[Graphics:HTMLFiles/3_ratkaisu_72.gif]

Out[34]=

Määrittele g(x)=-3x ja ratkaise yhtälö g(x)=4.

In[35]:=

Out[36]=

Määrittele funktio z(x,y)=sin(x y) cos(x y) ja piirrä se 3D-kuvana ja tasa-arvokäyrinä.

In[37]:=

[Graphics:HTMLFiles/3_ratkaisu_81.gif]

Out[38]=

[Graphics:HTMLFiles/3_ratkaisu_83.gif]

Out[39]=

Yhtälöiden ratkaiseminen

Ratkaise yleinen kolmannen asteen yhtälö
a x^3+b x^2+c x+d==0 käyttämällä reduce-komentoa.

In[40]:=

Out[40]=

(a≠0&& (xRoot[d + c #1 + b #1^2 + a #1^3&, 1] || xRoot[d + ... &x -d/c) || (d0&&c0&&b0&&a0)

Etsi yhtälön cos(x)=x ratkaisu.

In[41]:=

[Graphics:HTMLFiles/3_ratkaisu_88.gif]

Out[41]=

In[42]:=

Out[42]=

In[43]:=

Out[43]=

Ratkaise seuraava yhtälöryhmä
    3x+y=2
    y+2z=2
    x+z=1
symbolisesti ja numerisesti

In[44]:=

Out[44]=

Out[45]=

Out[46]=

Etsi yhtälöille
x^2+3 x-1= 0
3 x^2+5 x+1 = 0
symboliset ja numeeriset ratkaisut.

In[47]:=

$eqns = {x^2 + 3x - 10, 3x^2 + 5x + 10}$

Out[47]=

${-1 + 3 x + x^20, 1 + 5 x + 3 x^20}$

Out[48]=

Out[49]=

In[52]:=

$Plot[{x^2 + 3x - 1, 3x^2 + 5x + 1}, {x, -5, 3}]$

[Graphics:HTMLFiles/3_ratkaisu_111.gif]

Out[52]=

Ratkaise yhtälöryhmä
x^2+5 x-4 y=0
2 x-y=3
symbolisesti ja numeerisesti.

In[56]:=

$eqns = {x^2 + 5x - 4y0, 2x - y3}$

Out[56]=

${5 x + x^2 - 4 y0, 2 x - y3}$

Out[57]=

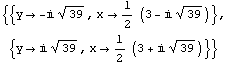
${{y - 39^(1/2), x1/2 (3 -  39^(1/2))}, {y 39^(1/2), x1/2 (3 +  39^(1/2))}}$

Out[58]=

In[59]:=

Out[59]=

Out[60]=

Out[61]=

Created by Mathematica (February 1, 2005)