Solution

In[63]:=

(*1*)Y = x * x * x + p * x * x + q * x + r0

Out[63]=

r + q x + p x^2 + x^30

In[64]:=

(*2*)Solve[Y, x]

Out[64]=

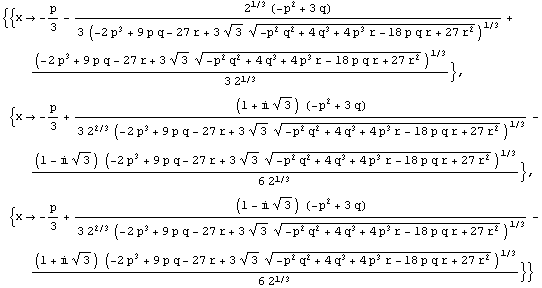
{{x -p/3 - (2^(1/3) (-p^2 + 3 q))/(3 (-2 p^3 + 9 p q - 27 r + 3 3^(1/2) (-p^2 q^2 + ... - 27 r + 3 3^(1/2) (-p^2 q^2 + 4 q^3 + 4 p^3 r - 18 p q r + 27 r^2)^(1/2))^(1/3))/(6 2^(1/3))}}

In[65]:=

(*3*)Y/.%Simplify[%]

Out[65]=

{r + q (-p/3 - (2^(1/3) (-p^2 + 3 q))/(3 (-2 p^3 + 9 p q - 27 r + 3 3^(1/2) (-p^2 q^2 + 4 q^ ... 3^(1/2) (-p^2 q^2 + 4 q^3 + 4 p^3 r - 18 p q r + 27 r^2)^(1/2))^(1/3))/(6 2^(1/3)))^30}

Out[66]=

{True, True, True}

Substituting a rule into an equation yields a logical expression, which can be simplified into another logical expression, which in this case is simply the expression True.

Created by Mathematica  (April 10, 2007) Valid XHTML 1.1!