Solution

In (a) the equations are all polynomial, so lets use Solve. For comparison, use also Reduce.

In[92]:=

(*a*)Clear[a, b, c] Solve[{a b + c0, c + a1, a b c1}, {a, b, c}] Reduce[{a b + c0, c + a1, a b c1}, {a, b, c}]

Out[93]=

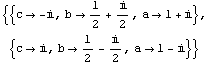
{{c -, b1/2 + /2, a1 + }, {c, b1/2 - /2, a1 - }}

Out[94]=

(a1 -  || a1 + ) &&ba/2&&c1 - a

The equations in (b) are all linear.

In[95]:=

(*b*)LinearSolve[{{1, 2, 3}, {0, 1, 1}, {0, -1, 1}}, {10, 1, 0}]

Out[95]=

{15/2, 1/2, 1/2}

In (c), it seems that we'll be needing FindRoot. However, let's try Solve. It gives a solution in terms of ProductLog. And, I'll be damned, the Solve solution is correct!

In[96]:=

(*c*)Solve[x Log[x] 10, x] %//NPlot[x Log[x] - 10, {x, .1, 8}] FindRoot[x Log[x] 10, {x, 6}]

InverseFunction :: ifun : Inverse functions are being used. Values may be lost for multivalued inverses. More…

Solve :: ifun : Inverse functions are being used by Solve, so some solutions may not be found; use Reduce for complete solution information. More…

Out[96]=

{{x10/ProductLog[10]}}

Out[97]=

{{x5.72893}}

[Graphics:../HTMLFiles/ex02_solutions_241.gif]

Out[98]=

⁃Graphics⁃

Out[99]=

{x5.72893}

Created by Mathematica  (April 10, 2007) Valid XHTML 1.1!