ex02_solutions

Solution

In[44]:=

(*1a*)Solve[x * x * x + x + 10, x] %//N

Out[44]=

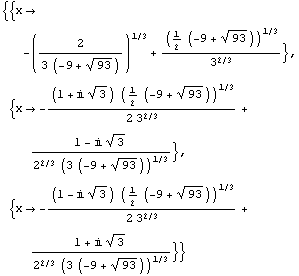
${{x -(2/(3 (-9 + 93^(1/2))))^(1/3) + (1/2 (-9 + 93^(1/2)))^(1/3)/3^(2/3)}, {x ... 9 + 93^(1/2)))^(1/3))/(2 3^(2/3)) + (1 +  3^(1/2))/(2^(2/3) (3 (-9 + 93^(1/2)))^(1/3))}}$

Out[45]=

In[46]:=

(*1b*)Solve[{x * x + y * y1, y2x + 1}, {x, y}] %//N

Out[46]=

Out[47]=

In[48]:=

(*2*)Eliminate[{x + y + z0, x y z1, x/z2}, z]

Out[48]=

See the help file for Eliminate for more info.

In[49]:=

(*3a*)Reduce[x^3 + p x^2 + q x + r0, x] ToRadicals[%]

Out[49]=

xRoot[r + q #1 + p #1^2 + #1^3&, 1] || xRoot[r + q #1 + p #1^2 + #1^3&, 2] || xRoot[r + q #1 + p #1^2 + #1^3&, 3]

Out[50]=

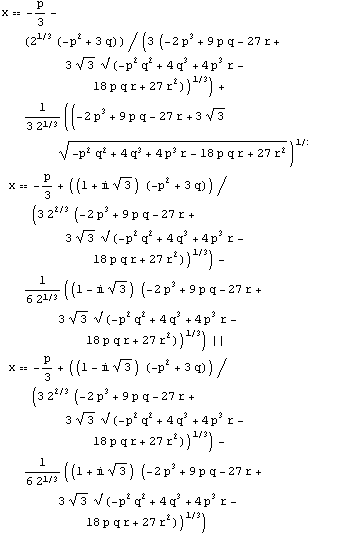
x -p/3 - (2^(1/3) (-p^2 + 3 q))/(3 (-2 p^3 + 9 p q - 27 r + 3 3^(1/2) (-p^2 q^2 + 4 ... q - 27 r + 3 3^(1/2) (-p^2 q^2 + 4 q^3 + 4 p^3 r - 18 p q r + 27 r^2)^(1/2))^(1/3))/(6 2^(1/3))

Here Reduce produces Root-objects, which are roots of a pure function, with argument #1. The Root-objects can be converted into the usual form with the function ToRadicals. This works always for polynomials of order 4 or less.

In[51]:=

Out[51]=

In[52]:=

Out[52]=

The same as 3a with a further restriction on x.

In[58]:=

$(*3d*)Clear[a] Reduce[{x^3 - a x^2 + x - a0, x>0}, x] Reduce[{x^3 - a x^2 + x - a0, a>0}, x]$

Out[59]=

Out[60]=

Note that the symbols are treated as complex numbers unless they appear explicitly in an inequality, or the assumption Element[x,Reals] is made.

In[61]:=

(*4*)Clear[a, b, c, d, e, x] Solve[a x * x * x * x + b x * x * x + c x * x + d x + e0, x]

Out[62]=

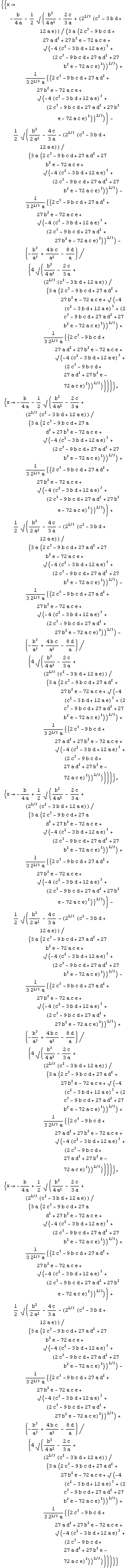
${{x -b/(4 a) - 1/2 √ (b^2/(4 a^2) - (2 c)/(3 a) + (2^(1/3) (c^2 - 3 b d + 12 a ... 2 a e)^3 + (2 c^3 - 9 b c d + 27 a d^2 + 27 b^2 e - 72 a c e)^2)^(1/2))^(1/3)/(3 2^(1/3) a))))}}$

In[63]:=

(*5*)Solve[x * x + p x + 10, x] Plot[x/.%[[1]], {p, 2, 6}]

Out[63]=

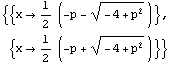
${{x1/2 (-p - (-4 + p^2)^(1/2))}, {x1/2 (-p + (-4 + p^2)^(1/2))}}$

[Graphics:../HTMLFiles/ex02_solutions_149.gif]

Out[64]=

Remember how to apply rules, and extract an element from a list? The function Solve gives a list of rules for x. Then, when we apply the rule to x, we get an expression featuring p and q. Note that the discriminant of the equation is negative for p<2. Plot will complain if you try to plot it. There's a similar situation in the next excercise.

In[65]:=

$(*6*)Solve[x * x + p x + q0, x] f[p_, q_] = x/.%[[1]] Plot3D[f[p, q], {p, -15, 15}, {q, -15, 15}, AxesLabel {p, q, f}]$

Out[65]=

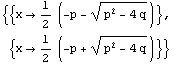
${{x1/2 (-p - (p^2 - 4 q)^(1/2))}, {x1/2 (-p + (p^2 - 4 q)^(1/2))}}$

Out[66]=

[Graphics:../HTMLFiles/ex02_solutions_158.gif]

Out[67]=

In[68]:=

Out[68]=

SolveAlways tries to find the values of all free parameters appearing in an equation, here a, b and c, for which the equation holds for all values of the variable, here x.

Created by Mathematica (April 10, 2007)