Excercise sheet 3
Interpolation
Tables
1. Make a table called DataA, that has as its elements ( ,
, 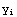 ) the following table
) the following table
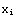
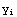
1 4.0
3 2.8
4 2.5
5 3.2
6 3.9
10 5.0
2. Make a table called DataB that has as its elements (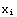 ,
, 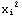 +10
+10 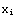 +1), where
+1), where  =0,1,2,...,5
=0,1,2,...,5
3. Read a table from file "data.dat" and assign it to DataC.
4. Plot the tables DataA, DataB, and DataC
5. Add to the start of the table DataA the element (0,6.0).
6. Add to the end of DataB the element (6, 0.0).
7. Insert (2, 3.4) between the third and fourth element of DataA.
Solutions
Interpolating functions
First
1. Make a table that has as its elements (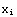 ,
, 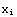 exp(-
exp(-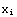 )), where
)), where 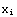 =0,1/2,1,3/2...,5. Assign the symbol A to the table (A=Table[...])
=0,1/2,1,3/2...,5. Assign the symbol A to the table (A=Table[...])
2. Print out the contents of table A using the TableForm[...] function.
3. Make an interpolating polynomial to table A.
4. Calculate the value of the polynomial at points x=0, 1, 2.5 and compare the results with the corresponding values in table A
5. Plot the interpolating polynomial and the function x 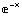 into the same picture.
into the same picture.
6. Plot the difference of the interpolating polynomial and the function x 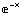 .
.
Solutions
Second
1. Read the file "data.dat" into table A.
2. Make an interpolating function to table A.
3. Plot the interpolating function.
4. Make an spline interpolating function to table A.
5. Plot the spline function.
Solutions
Third -- An evil example - this shows that you have to be careful with the interpolating polynomial!
1. Make a table (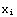 ,
, 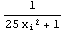 ), where
), where 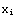 =-1,-0.8,..., 0.8, 1.
=-1,-0.8,..., 0.8, 1.
2. Make an interpolating polynomial to the table
3. Make an interpolating function to the table
4. Plot the interpolating function and polynomial in the same figure. What do you see? Try increseasing / decresing the step length when making the table. You can also try making a spline fit to the table. Try plotting that in the same figure also.
Solutions
Least squares fitting
Fit-command
1. Fit a second order polynomial to the data in the following table, and plot the data points and the fit.
| -2 |
2.84` |
| -1 |
0.86` |
| 0 |
1.09` |
| 1 |
2.5100000000000002` |
| 2 |
7.17` |
2. Fit the function a sin(x) + b cos(x)to the data in the following table, and plot the data points and the fit.
| 0 |
1.04` |
| 2 |
0.44` |
| 4 |
-1.51` |
| 6 |
0.6` |
| 8 |
0.78` |
| 10 |
-1.45` |
Solutions
Regress-command
1. Fit a straight line a x+b to following data, and get the standard error in a and b
| -1 |
-0.5` |
| 0 |
1.2000000000000002` |
| 1 |
2.8000000000000003` |
| 2 |
4.9` |
2. Fit the function a+b  +c x
+c x  to following data, and get the standard error for a, b and c
to following data, and get the standard error for a, b and c
| 0 |
1.6` |
| 0.5` |
3.8000000000000003` |
| 1.` |
6.300000000000001` |
| 1.5` |
12.700000000000001` |
| 2.` |
22.900000000000002` |
Solutions