Excercise sheet 5

Revision Excercises (before attacking differential equations)

One

1.    Construct a table of series of the cosine function, of different orders, at least a dozen of them. Plot them in the same picture, with different colours. Figure out how you can set the colours as a table.
2.    Experiment with the Select function. Construct a table of random numbers from the interval [1,6], and pick out all the sixes therefrom.
3.    Get familiar with the Cases function. Construct the set {x,x^2,e^y,x+y,5x,x^x^x,sin x,log x+cos x}or make your own, with a lot of different kind of expressions. Then pick out all expressions which are in the form of x^y. Also try out the Levelspec option.

Solutions

Two

1.    Experiment with the options of Plot. Find out how you can label the axes, change the font and font size. Then change the background color.
2.    Plot the trajectory (x(t),y(t))=(cos t,sin t) in (x,y)-plane. Then plot the trajectory (x(t),y(t),z(t))=(t,cos t,sin t) in (x,y,z)-plane. Find out
how you can change the viewpoint.

Solutions

Three!

This excercise should be made with a computer with speakers.
1.    Check the help file for the function Play.

Solutions

Differential Equations

First

Solve the following linear first order differential equations
3.1.    y'(x)+3y(x)=2, y(0)=1
3.2.    x'(t)+sin(t) x(t)=0, x(0)=-1. Also plot the solution x(t) for 0<t<3
3.3.    f'(x)+p(x)f(x)=q(x), find the general solution.

Solutions

Second

Solve the following second-order linear differential equations
3.4.    y''(t)+3y'(t)-2y(t)=1, y'(0)=1, y(0)=0, plot the real part of the solution.
3.5.    f''(x)+x f(x)=0, f'(0)=1, f(0)=2, solve both numerically and analytically.
3.6.    x''(t)+(a-2q cos(2t))x(t)=0.

Solutions

Third

Solve the following nonlinear differential equations. If DSolve does not give you an analytic solution, find the solution numerically.
3.7.    y'(t)+y(t)^2=0, y(0)=2, plot the solutions for 0<t<10
3.8.    θ''(t)+1/10θ'(t)+2sin(θ(t))=3cos(2t), plot the solution for 0<t<10π

Solutions

Fourth

3.9. Additional extra-fun excercise! Solve the following nonlinear set of differential equations (known as the Lorenz equations):
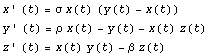
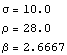
    x ' (t) = σ x(t) (y(t) - x(t))  y ' (t) = ρ x(t) - y(t) - x(t) z(t)  z ' (t) = x(t) y(t) - β z(t)        σ = 10.  ρ = 28.  β = 2.6667
You can try to plot the solution as a three dimensional curve using ParametricPlot3D.    

Solutions

Created by Mathematica  (April 10, 2007) Valid XHTML 1.1!