Excercise sheet 6 -- solutions
1. A baseball in free-fall
Continue the example of the lecture notes on the example for a baseball thrown straight up. We solved the equation
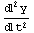 =a=g,
=a=g,
with the initial conditions
y(t=0)=0.
1.1. We were left with one constant undefined. Fix that constant by using the additional initial condition
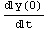 =
=![Overscript[y, .]](HTMLFiles/ex06_solutions_3.gif) (0)=10m/s.
(0)=10m/s.
1.2. Find the highest point of the ball's path and the moment when the ball returns to the height it was thrown from.
Solutions
2. A brick falling in water
Continue the example on the brick dropped from a boat. Our differential equation for the position y of the brick was
F=m g-k ![Overscript[y, .]](HTMLFiles/ex06_solutions_9.gif) =m
=m ![Overscript[y, ..]](HTMLFiles/ex06_solutions_10.gif) .
.
2.1. Set some sensible initial conditions for the brick's position, (i) solve the equation and give the constant some numeric values. (ii) Plot the solution. What do you find? Study the effect of changing the mass of the brick without chaning the coefficent k. (iii) Find the terminal velocity of the falling brick (hint: use the Limit-command, to tell that m and k are positive, give Assumptions→{k>0, m>0} to the command).
2.2. Solve the brick example numerically. Compare the numerical solution to the analytic one by plotting both solutions, or by comparing the values of ygiven by the two solutions.
Solutions
3. Flying rocket
3.1. Solve the rocket example, and plot the solution, but this time take into account the force due to air-resistence, 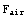 =-k
=-k 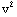 =-k
=-k ^2](HTMLFiles/ex06_solutions_22.gif) . Use k=0.3 in your calculations. Is the equation of motion still linear? Compare the path of this rocket to the one studied in the examples.
. Use k=0.3 in your calculations. Is the equation of motion still linear? Compare the path of this rocket to the one studied in the examples.
Solutions
4. Frictionless and damped oscillators
4.1 Solve the frictionless
m ![Overscript[x, ..]](HTMLFiles/ex06_solutions_26.gif) +k x=0
+k x=0
and damped
m ![Overscript[x, ..]](HTMLFiles/ex06_solutions_27.gif) +γ
+γ ![Overscript[x, .]](HTMLFiles/ex06_solutions_28.gif) +k x=0
+k x=0
oscillators with the same initial conditons. Plot both of them in the same coordinates. What do you find? Does the damping affect the frequency of the oscillations?
Solutions
5. LC- and LCR-circuits
5.1. Continue the example on the LCR-circuits. The general analytic solution was given in the lecture notes. Now fix the constants and study the behaviour of the system by plotting the solutions. Vary the values for the components and see what happens.
Solutions