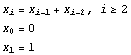Excercise sheet 8 -- solutions
Loops
1. What is the difference between the While and Do loops that were presented in the lecture notes?
2. Write the Mathematica commands to calculates the n first Fibonacci numbers, defined according to the relation
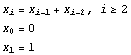
ie, each Fibonacci number is the sum of two previous ones. Ask the number n from the user. To print out the numbers you can use the Print-command.
3. Calculate the sum ![Underoverscript[∑, i = 0, arg3]](HTMLFiles/ex08_solutions_2.gif)
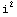 using Do- and While loops.
using Do- and While loops.
4. The Hénon map. Make a loop that iterates the famous Hénon map
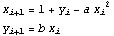 ,
,  .
.
Try if you can store the results in a list of points ( ,
,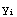 ) and plot those! (You can use the Append command to add (x,y) pairs to a list)
) and plot those! (You can use the Append command to add (x,y) pairs to a list)
Solutions
Nest and FixedPoint
The Nest and FixedPoint commands are useful when one needs to iterate a function. Say you have a function f, and you need to apply it n times to a number 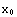 , that is, you want to compute
, that is, you want to compute
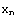 =
=![Underscript[Underscript[f(f(⋯ f(f(x_0)) ⋯)), ︸], n applications of f]](HTMLFiles/ex08_solutions_34.gif) =
=![Underscript[Underscript[(f ◦ f ◦ ⋯ ◦ f), ︸], n]](HTMLFiles/ex08_solutions_35.gif) (
(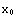 ).
).
This is called nesting and to evaluate these in Mathematica, you can use the Nest command:
Nest[f, x0, n],
where f is your function (must be a pure function, not a Mathematica expression!), x0 the argument for the innermost f, and n is the number of iterations.
1. Implement the loops of previous excersise using the Nest command.
2. Find the square root of 10 using the Newton's method and the Nest-command. If you've an equation g(x)=0, and a guess 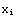 for its solution, Newton's method gives you an improved guess
for its solution, Newton's method gives you an improved guess 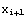 for the solution:
for the solution:
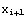 =f(
=f(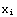 )=
)=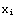 -
-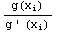 .
.
When f is applied repeatedly, you end up with better and better approximations for the solution (we're ignoring the important matter of convergence here, of course).
To find the square root of a, the function g(x)=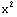 -a, and
-a, and
(1) f(x)=x-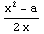 .
.
So, set a=10, and apply the Nest command to f(x). Set the initial guess 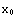 to your liking and try different values of n. Compare the results to Sqrt[10].
to your liking and try different values of n. Compare the results to Sqrt[10].
The command FixedPoint works the same way as Nest, but you don't give the number of iterations as an argument. Instead, Mathematica applies the function f so many times that the result does not change, i.e. it tries to find the limit
x=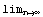
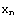 ,
,
This x is called a fixed point, since it satisfies f(x)=x, hence the name of the command. Try the FixedPoint command with the function f from Eq. (1). Compare the result to 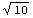 .
.
Solutions
1
2
Rocket science
Make the rocket example two dimensional, ie. take into account that the rocket can move in two directions. With some simplifications we can take the equations of motion to be
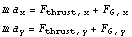
Assume again that the thrust  is constant. Let us take the direction of this force to be the same as the velocity of the rocket. In this case, the force vector reads
is constant. Let us take the direction of this force to be the same as the velocity of the rocket. In this case, the force vector reads
![Overscript[F, _] _thrust](HTMLFiles/ex08_solutions_71.gif) =(
=( ,
,  )=
)= (
(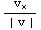 ,
, 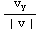 ),
),
where
|v|=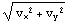 ,
.
,
.
Earth's gravity is naturally directed towards the center of the planet, so gravity reads
![Overscript[F, _] _grav](HTMLFiles/ex08_solutions_80.gif) =m g (
=m g (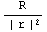 )
)![Overscript[r, _]/(| r |)](HTMLFiles/ex08_solutions_82.gif) ,
,
where r=(x, y), and |r|=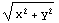 . Note that we've taken the positions to be relative to the center of the mass, not to the surface of the planet.
. Note that we've taken the positions to be relative to the center of the mass, not to the surface of the planet.
Solution
Mandelbrot set
The Mandelbrot set is defined as the set of points c for which the sequence defined by
(1) 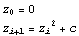
does not approach infinity. Construct a function that counts the number of iterations of (1) that are required for the absolute value of z to become larger than 2. You also need to limit maximum number of iterations allowed. Then make a 3D plot of the function by taking the real and imaginary parts of c to be the x and y coordinates of the plot. The result should be a rather familiar looking object.
Solution