1
So, we are trying to solve the equation
-y''(r)- y(r)=E y(r),
y(r)=E y(r),
or, more specifically, the first excited state of this.
First, a few words on the excited states. The discrete states of a quantum mechanical system can be characterized by so-called quantum numbers, which then serve to determine the energy, momentum, angular momentum etc. of the system. Suppose a system is completely determined by its energy, or its energy quantum number. This applies well to the states in question here, i.e. the lowest energy states of the hydrogen atom. The energy levels of the system, in this case the electron, are of the form
f(k), where k is the energy quantum number. The range of possible values of k determines the range of the energy values.
Usually, in numerical calculations, we don't know the function f. From the outset of the problem, from the zero of the Coulomb potential, we can however deduce that E<0, so as k increases, the energy approaches zero from below. The ground state energy was found to be -1, so all (an infinite number of) excited states are in the interval -1<E<0. There is, a priori, no way of telling where the 'second' state is. The only way of finding out is to calculate the values of the function Δ(E) in sufficiently small steps, starting from -1 and see where its next zero lies.
What is the significance of the function Δ, defined as
Δ(E)= -
- ,
,
where 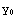 (r) is the solution in the interval
(r) is the solution in the interval 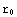 <r<
<r< and
and 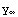 (r) gives the solution for
(r) gives the solution for  <r<
<r<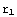 ? Here
? Here 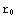 is the point corresponding to the origin in our numerical calculations, and
is the point corresponding to the origin in our numerical calculations, and 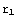 corresponds to infinity (actual zero and infinity are hard to handle in numerics). The solution of the above equation starts from the formulation of the boundary conditions, in this case they are y(
corresponds to infinity (actual zero and infinity are hard to handle in numerics). The solution of the above equation starts from the formulation of the boundary conditions, in this case they are y(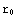 )=
)=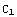
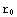 and y(
and y(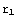 )=
)=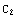
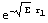 , where
, where 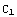 and
and 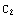 are some constants, which are determined by matching of the partial solutions and the normalization (for the beginning part of the solution, these constants can be set to unity). Corresponding to these boundary conditions, the differential equation has solutions only for a certain set of values of E. A possible solution y of the equation, corresponding to some (guessed) value of E, has to satisfy the conditions that y and y' are continuous, i.e.
are some constants, which are determined by matching of the partial solutions and the normalization (for the beginning part of the solution, these constants can be set to unity). Corresponding to these boundary conditions, the differential equation has solutions only for a certain set of values of E. A possible solution y of the equation, corresponding to some (guessed) value of E, has to satisfy the conditions that y and y' are continuous, i.e. 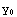 (
( )=
)=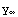 (
( ) and
) and 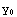 '(
'( )=
)=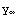 '(
'( ). Dividing these equations yields the condition that Δ(E)=0. What this all means is that if Δ(E)≠0, there are no solutions corresponding to this value of E.
). Dividing these equations yields the condition that Δ(E)=0. What this all means is that if Δ(E)≠0, there are no solutions corresponding to this value of E.
Alright, let's get on with the solution. First, we'll input some definitions. The crucial ones here are the values of r demarcating the different regions. With an inappropriate choice of 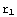 , the function Δ might behave in a way making it difficult to find the zeros. Again, there is no way of telling what is an appropriate choice, but as a rule, you should make
, the function Δ might behave in a way making it difficult to find the zeros. Again, there is no way of telling what is an appropriate choice, but as a rule, you should make 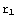 large enough and
large enough and  not too large. In the second excercise, a better way of finding the zeros of Δ is presented. Note also that the constants
not too large. In the second excercise, a better way of finding the zeros of Δ is presented. Note also that the constants 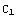 and
and 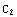 have been set equal to one in the boundary condition functions y0 and y1.
have been set equal to one in the boundary condition functions y0 and y1.
In[1]:=
![Clear[e, eq] ;](../HTMLFiles/ex09_solutions_33.gif)
![eq := -y''[r] - 2/ry[r] e y[r] ;](../HTMLFiles/ex09_solutions_34.gif)
![y0[r_] = r ; dy0[r_] = D[y0[r], r] ;](../HTMLFiles/ex09_solutions_36.gif)
![y1[r_] = Exp[-(-e)^(1/2) r] ; dy1[r_] = D[y1[r], r] ;](../HTMLFiles/ex09_solutions_37.gif)
Then, give some off-the-hat values to E and calculate the corresponding value of Δ. You can do this simply by hand, setting one value after the other, or devise some neat automatic method. For example, you could give E the values -0.9,-0.8,... ,-0.2 and discover that Δ(E) changes sign in the interval -0.3<E<-0.2.
In the following, diff1=Δ(e1) and diff2=Δ(e2).
In[6]:=
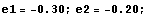
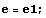
![sol0 = Part[NDSolve[{eq, y[r0] y0[r0], y '[r0] dy0[r0]}, y[r], {r, r0, rinter}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_40.gif)
![sol1 = Part[NDSolve[{eq, y[r1] y1[r1], y '[r1] dy1[r1]}, y[r], {r, rinter, r1}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_41.gif)
![u0[r_] = y[r]/.sol0 ; u1[r_] = y[r]/.sol1 ;](../HTMLFiles/ex09_solutions_42.gif)
![d0[r_] = D[u0[r], r]/u0[r] ; d1[r_] = D[u1[r], r]/u1[r] ;](../HTMLFiles/ex09_solutions_43.gif)
![Print["diff1 = ", diff1 = d0[rinter] - d1[rinter]]](../HTMLFiles/ex09_solutions_44.gif)
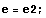
![sol0 = Part[NDSolve[{eq, y[r0] y0[r0], y '[r0] dy0[r0]}, y[r], {r, r0, rinter}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_46.gif)
![sol1 = Part[NDSolve[{eq, y[r1] y1[r1], y '[r1] dy1[r1]}, y[r], {r, rinter, r1}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_47.gif)
![u0[r_] = y[r]/.sol0 ; u1[r_] = y[r]/.sol1 ;](../HTMLFiles/ex09_solutions_48.gif)
![d0[r_] = D[u0[r], r]/u0[r] ; d1[r_] = D[u1[r], r]/u1[r] ;](../HTMLFiles/ex09_solutions_49.gif)
![Print["diff2 = ", diff2 = d0[rinter] - d1[rinter]]](../HTMLFiles/ex09_solutions_50.gif)
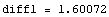
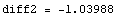
Now, since diff1 and diff2 have opposite signs, it has to be the case that Δ(E)=0 for some value of E for which e1<E<e2. We will search a more accurate approximation of the eigenvalue by dividing the interval [e1,e2] in half and calculate Δ(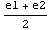 ), from the sign of which we can then deduce the location of the eigenvalue with double precision, i.e. it is either in the interval [e1,
), from the sign of which we can then deduce the location of the eigenvalue with double precision, i.e. it is either in the interval [e1,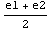 ] or [
] or [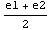 ,e2]. This process of dividing the interval in half is then repeated until some predefined, desired accuracy is reached.
,e2]. This process of dividing the interval in half is then repeated until some predefined, desired accuracy is reached.
To decide which of the subintervals to examine next, we calculate the product diff*diff1, where diff stands for Δ(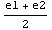 ). If this product is negative, it means that diff and diff1 have different signs and the eigenvalue must lie between e1 and
). If this product is negative, it means that diff and diff1 have different signs and the eigenvalue must lie between e1 and 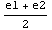 . If it is positive, the eigenvalue is in the other interval.
. If it is positive, the eigenvalue is in the other interval.
In[19]:=
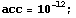
![While[Abs[e1 - e2] >acc, e = (e1 + e2)/2 ; sol0 = Part[NDSolve[{eq, y[r0] ... nter] ; If[diff * diff1 >= 0, e1 = e ; diff1 = diff, e2 = e ; diff2 = diff ;] <br />]](../HTMLFiles/ex09_solutions_59.gif)
![Print["eigenvalue = ", e]](../HTMLFiles/ex09_solutions_60.gif)
![Print["difference of the logarithmic derivatives = ", diff]](../HTMLFiles/ex09_solutions_61.gif)
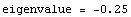

This solution can be verified by comparison with the analytical solution, 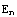 =
=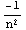 , i.e.
, i.e. 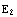 =-
=-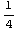 .
.
Then we can construct the wave function. A preliminary solution has been calculated above: y(r)={
. This is however not yet satisfactory. The matching is not perfect, because the condition Δ(E)=0 allows any possible constants to be cancelled out. We need two constants, one for the matching and one for normalization of the wave function.
In[23]:=
![fig0 = Plot[u0[r], {r, r0, rinter}, DisplayFunctionIdentity] ;](../HTMLFiles/ex09_solutions_70.gif)
![fig1 = Plot[u1[r], {r, rinter, 15}, DisplayFunctionIdentity] ;](../HTMLFiles/ex09_solutions_71.gif)
![Show[fig0, fig1, DisplayFunction$DisplayFunction] ;](../HTMLFiles/ex09_solutions_72.gif)
![[Graphics:../HTMLFiles/ex09_solutions_73.gif]](../HTMLFiles/ex09_solutions_73.gif)
We'll start the search of the constant from the normalization condition. We'll denote y(r)={
. Then the normalization condition becomes
1=![Underscript[∫, V]](../HTMLFiles/ex09_solutions_76.gif) |ψ(r)
|ψ(r)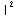 dV=
dV=![Underscript[∫, Ω]](../HTMLFiles/ex09_solutions_78.gif) dΩ
dΩ![Overscript[Underscript[∫, 0], ∞]](../HTMLFiles/ex09_solutions_79.gif)
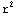 dr
dr 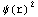 =4π
=4π![Overscript[Underscript[∫, 0], ∞]](../HTMLFiles/ex09_solutions_82.gif)
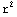
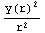 dr
dr
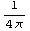 =
=![Overscript[Underscript[∫, r_0], r_1]](../HTMLFiles/ex09_solutions_86.gif)
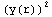 dr=
dr=![Overscript[Underscript[∫, r_0], r_inter]](../HTMLFiles/ex09_solutions_88.gif)
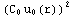 dr+
dr+![Overscript[Underscript[∫, r_inter], r_1]](../HTMLFiles/ex09_solutions_90.gif)
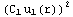 dr=
dr=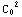 (
(![Overscript[Underscript[∫, r_0], r_inter]](../HTMLFiles/ex09_solutions_93.gif)
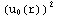 dr+
dr+![Overscript[Underscript[∫, r_inter], r_1]](../HTMLFiles/ex09_solutions_95.gif)
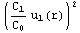 dr).
dr).
Then, denote 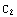 =
=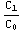 , and the matching condition
, and the matching condition 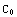
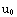 (
( )=
)=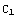
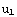 (
( ) becomes
) becomes 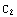 =
= .
.
In[26]:=
![C2 = u0[rinter]/u1[rinter] ;](../HTMLFiles/ex09_solutions_107.gif)
![fig0 = Plot[u0[r], {r, r0, rinter}, DisplayFunctionIdentity] ;](../HTMLFiles/ex09_solutions_108.gif)
![fig1 = Plot[C2 u1[r], {r, rinter, 15}, DisplayFunctionIdentity] ;](../HTMLFiles/ex09_solutions_109.gif)
![Show[fig0, fig1, DisplayFunction$DisplayFunction] ;](../HTMLFiles/ex09_solutions_110.gif)
![[Graphics:../HTMLFiles/ex09_solutions_111.gif]](../HTMLFiles/ex09_solutions_111.gif)
Then we calculate the normalization coefficient. Note that the actual wave function is the function y(r)/r. That is plotted in the following.
In[30]:=
![nn = NIntegrate[u0[r]^2, {r, r0, rinter}] + NIntegrate[(C2 u1[r])^2, {r, rinter, r1}] ; C0 = 1/Sqrt[4π nn] ;](../HTMLFiles/ex09_solutions_112.gif)
![fig0 = Plot[C0 u0[r]/r, {r, r0, rinter}, DisplayFunctionIdentity] ;](../HTMLFiles/ex09_solutions_113.gif)
![fig1 = Plot[C0 C2 u1[r]/r, {r, rinter, 15}, DisplayFunctionIdentity] ;](../HTMLFiles/ex09_solutions_114.gif)
![Show[fig0, fig1, DisplayFunction$DisplayFunction] ;](../HTMLFiles/ex09_solutions_115.gif)
![[Graphics:../HTMLFiles/ex09_solutions_116.gif]](../HTMLFiles/ex09_solutions_116.gif)
This can then be compared to the analytical solution. In Wikipedia, there is some visualization of the orbitals, and you can do a comparison if you wish. http://en.wikipedia.org/wiki/Hydrogen_atom#Visualizing_the_hydrogen_electron_orbitals
![sol0 = Part[NDSolve[{eq, y[r0] y0[r0], y '[r0] dy0[r0]}, y[r], {r, r0, rinter}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_40.gif)
![sol1 = Part[NDSolve[{eq, y[r1] y1[r1], y '[r1] dy1[r1]}, y[r], {r, rinter, r1}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_41.gif)
![sol0 = Part[NDSolve[{eq, y[r0] y0[r0], y '[r0] dy0[r0]}, y[r], {r, r0, rinter}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_46.gif)
![sol1 = Part[NDSolve[{eq, y[r1] y1[r1], y '[r1] dy1[r1]}, y[r], {r, rinter, r1}, AccuracyGoal15], 1] ;](../HTMLFiles/ex09_solutions_47.gif)
![While[Abs[e1 - e2] >acc, e = (e1 + e2)/2 ; sol0 = Part[NDSolve[{eq, y[r0] ... nter] ; If[diff * diff1 >= 0, e1 = e ; diff1 = diff, e2 = e ; diff2 = diff ;] <br />]](../HTMLFiles/ex09_solutions_59.gif)
![Print["difference of the logarithmic derivatives = ", diff]](../HTMLFiles/ex09_solutions_61.gif)
![[Graphics:../HTMLFiles/ex09_solutions_73.gif]](../HTMLFiles/ex09_solutions_73.gif)
![[Graphics:../HTMLFiles/ex09_solutions_111.gif]](../HTMLFiles/ex09_solutions_111.gif)
![nn = NIntegrate[u0[r]^2, {r, r0, rinter}] + NIntegrate[(C2 u1[r])^2, {r, rinter, r1}] ; C0 = 1/Sqrt[4π nn] ;](../HTMLFiles/ex09_solutions_112.gif)
![[Graphics:../HTMLFiles/ex09_solutions_116.gif]](../HTMLFiles/ex09_solutions_116.gif)