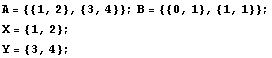
ex10_solutions

In[1]:=

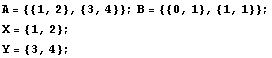
A = {{1, 2}, {3, 4}} ; B = {{0, 1}, {1, 1}} ; X = {1, 2} ; Y = {3, 4} ;

In[2]:=

(*a*)Print["AB = ", A . B//MatrixForm] Print["BA = ", B ... uot;AB-BA = ", A . B - B . A//MatrixForm, ". This is the commutator of A and B."]

AB-BA =  ( {{-1, -1}, {0, 1}} ) . This is the commutator of A and B.

In[7]:=

Out[7]=

In[8]:=

(*c*)Z = LinearSolve[A, X] ; Print["Z = ", Z//MatrixForm] Print["AZ = ", A . Z//MatrixForm, ", X = ", X//MatrixForm]

In[11]:=

-1 -1 ... Form] Print[A A = , Inverse[A] . A//MatrixForm,, AA = , A . Inverse[A]//MatrixForm]

In[13]:=

In[14]:=

(*f*)Print["The eigenvalues of A are ", Eigenvalues[A][[1]], " and &q ... vectors[A][[1]]//MatrixForm, " and ", Eigenvectors[A][[2]]//MatrixForm, "."]

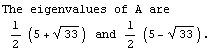
The eigenvalues of A are 1/2 (5 + 33^(1/2))  and 1/2 (5 - 33^(1/2))  .

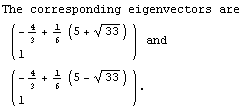
$The corresponding eigenvectors are  ( {{-4/3 + 1/6 (5 + 33^(1/2))}, {1}} )  and  ( {{-4/3 + 1/6 (5 - 33^(1/2))}, {1}} )  .$

In (g), we'll assume that the third component of X and Y is zero (in order to get the familiar cross product).

In[16]:=

(*g*)X = Append[X, 0] ; Y = Append[Y, 0] ; Print["XY = ", Cross[X, Y]//MatrixForm]

Created by Mathematica (April 10, 2007)