Excercise sheet 4 -- solutions
Derivatives
1. Derivate 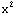 +4xwith respect to x
+4xwith respect to x
2. Derivate 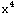 +3x-sin(x) twice
+3x-sin(x) twice
3. Let the position of a moving body be given by the expression x(t) = 40-5t-5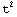 . What is the position, velocity and the acceleration at t=2
. What is the position, velocity and the acceleration at t=2
4. Plot the velocity and position of the previous task in same figure.
5. Does Mathematica know the most common rules for taking derivatives? Find the derivative of
a. f(g(x)) (chain rule)
b. f(x) g(x) (derivative of a product)
c. 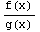 (derivative of a fraction)
(derivative of a fraction)
6. Let f(x,y)=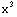
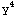 . Find the partial derivatives
. Find the partial derivatives
a. 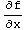 ,
, 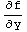
b. 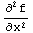 ,
, 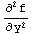
c. 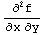 ,
, 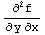
Solutions
Total differential
1.
1. Find the total differential of F(x,y,z)=x y+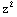 x+y
x+y 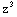
2. Find the total differential of G(r, θ,φ)=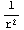 sin(θ)cos(φ).
sin(θ)cos(φ).
3. Find the total derivative of F(x, y)=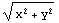 , x=x(t), y=y(t), with respect to t
, x=x(t), y=y(t), with respect to t
Solutions
2.
Let U(S,V,N)=T S-p V+μ N. This is the internal energy of a system with state variables entropy S, volume V and particle number N.
1. Find the total differential of U.
2. Find the partial derivative 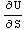 and
and 
3. Find the total derivatives  and
and 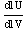
4. Take the total differential of U and set the differentials with respect to T, p and μ to zero.
Solutions
3.
1. Sven-Erik finds a mysterious metal sphere on his lawn. He measures the radius of the sphere three times, and gets as results r=12.0, 12.1, 11.8 centimeters. Find the volume of the sphere V=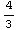 π
π 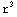 and the error limits.
and the error limits.
2. Let's assume that the number of monkeys at a zoo depends on the number of bananas and the weight of a monkey according to the following formula: m[banana_,weight_]=3*banana/weight. Calculate the number of monkeys and the error limits when there are 100 ± 5 kg of bananas and one monkey weighs 7.3 ± 1.2 kg!
Solutions
Integration
1.
1. Integrate sin(x), x=0 ... 2π. Find also the numerical value.
2. Integrate ln x, check the result by taking its derivative
3. Find the definite integral 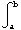 (
(
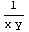 dx)dy.
dx)dy.
4. A car is speeding at a velocity of v=15m/s. The police starts chasing the car, accelerating at a=10m/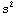 . When does the police catch the speeding man? Plot the positions of both cars as a function of time.
. When does the police catch the speeding man? Plot the positions of both cars as a function of time.
5. The acceleration of a moving body is given by the expression a(t)=arctan(t), where t is the time in seconds. Find the average velocity over the first twelve seconds, assuming the particle starts at rest at t=0.What is the velocity after 20 seconds?
Solutions
Limits and series
1.
Find the following limits
1. 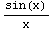 , x→0
, x→0
2. 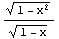 ,x→1
,x→1
3. 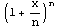 ,n→∞
,n→∞
4. 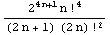 ,n→∞
,n→∞
Solutions
2.
1. Find the Taylor series of 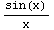 up to order 5.
up to order 5.
2. Find the Taylor series of sin(x) up to 2nd, 5th, and 9th orders, and plot each of the together with the sine function to the same figure.
3. Expand an undefined function, say f(x), as a power series. What do you find?
4. As an example of a Laurent series, expand the function f(x)=tan(x) as series around the point 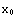 =π/2. Compare the result to the fraction of the power series of sin(x) and cos(x) expanded around the same point.
=π/2. Compare the result to the fraction of the power series of sin(x) and cos(x) expanded around the same point.
5. Functions can have Laurent series expressions around the point 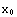 =∞ also. As an example, find the Laurent series of the function
=∞ also. As an example, find the Laurent series of the function 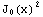 around the point
around the point 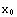 =∞up to second order.
=∞up to second order.  (x) is the zeroth order Bessel J function, given in Mathematica by the BesselJ[0,x] function. Plot the series and the original function in same figure.
(x) is the zeroth order Bessel J function, given in Mathematica by the BesselJ[0,x] function. Plot the series and the original function in same figure.
6. Show that the relativistic expression for energy, E=m 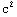 , reduces at the low velocity limit to the non-relativistic kinetic energy, E=
, reduces at the low velocity limit to the non-relativistic kinetic energy, E=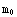
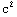 +
+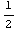 m
m 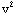 , when we take the relationship between the mass m of a moving body and rest mass
, when we take the relationship between the mass m of a moving body and rest mass 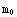 to be m=
to be m=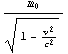 , as given by the theory of relativity.
, as given by the theory of relativity.
Solutions
